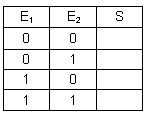
Les interrupteurs
représentent
les
entrées. L'entrée est à 1 si
l'interrupteur
est actionné.
La lampe représente la sortie. La sortie est à 1 si la lampe est allumée.
La lampe représente la sortie. La sortie est à 1 si la lampe est allumée.
a/
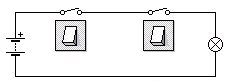
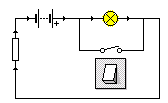
Etablir
la table de vérité de chacun des montages
ci-dessous puis lui associer l'une des 4 fonctions logiques
proposées :
NON
(NOT) ; ET
(AND) ; OU (OR) ; OU EXCLUSIF (XOR).
Aide
: écrire
à quelle(s) condition(s) la sortie est à 1.
 |
 |
 |
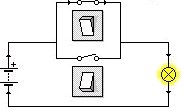 |
| fig 1 | fig 2 | fig 3 | fig 4 |
Les fonctions NON-ET (NAND) et NON-OU (NOR) ont les TV suivantes.
b/
Justifier
rapidement leurs noms.
1.2. En utilisant des circuits intégrés : portes logiques
|
Mise en oeuvre des circuits intégrés. Il s'agit de
circuits électroniques réalisant une
fonction logique. Ces circuit se présentent sous la forme de
boitiers
pleins rectangulaires noirs. Ils sont équipés de
broches/pattes
numérotées qui leurs permettent
d'établir des
connexions. L'affectation
de chacune des pattes s'appelle le brochage.
Les circuits que vous allez utiliser comportent 14 pattes. Ils appartiennent à la série 4000 en technologie cmos et contiennent chacun 4 fois la même porte logique. Il s'agit des circuits intégrés (CI) 4081 ; 4071 ; 4030 et 4011. Ci-contre est présenté le brochage (en norme américaine à gauche et europénne à droite) du 4011. Pour la mise en oeuvre, suivre les explications du professeur et répondre aux questions. |
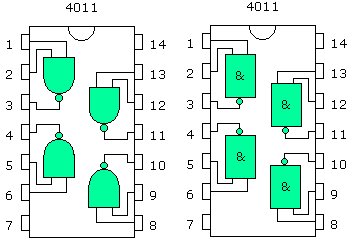 |
2/ Addition binaire : combinaison de fonction logique simple
Il
permet l'addtion des bits de
plus faible poids (rang 0) de 2 nombres binaires

R0 désigne une éventuelle retenue.
a/ Compléter la table de vérité ci-dessous en faisant les additions correspondantes :
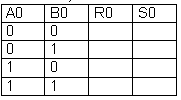
b/ Exprimer S0 en fonction de A0 et B0 en utilisant une fonction logique simple.
c/ Même question pour R0.
d/ Reproduire et compléter alors le montage ci-dessous :
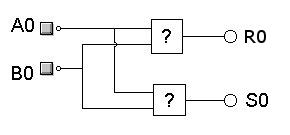
e/ Réaliser le montage sur platine d'essai et appeler pour vérification.
f/ Vérifier la table de vérité obtenue en a/
Ce montage ne permet pas de tenir compte d'une éventuelle retenue. Il ne peut donc pas être utilisé pour autre chose que l'addition des bits de rang 0 (les unités). Pour ajouter les bits de rang 1 (que l'on pourrait appelés les deuzaines) et plus (les quatraines, les huitaines...), il faut un montage combinant 2 demi-additionneurs : l'additionneur complet.

R0 désigne une éventuelle retenue.
a/ Compléter la table de vérité ci-dessous en faisant les additions correspondantes :

b/ Exprimer S0 en fonction de A0 et B0 en utilisant une fonction logique simple.
c/ Même question pour R0.
d/ Reproduire et compléter alors le montage ci-dessous :

e/ Réaliser le montage sur platine d'essai et appeler pour vérification.
f/ Vérifier la table de vérité obtenue en a/
Ce montage ne permet pas de tenir compte d'une éventuelle retenue. Il ne peut donc pas être utilisé pour autre chose que l'addition des bits de rang 0 (les unités). Pour ajouter les bits de rang 1 (que l'on pourrait appelés les deuzaines) et plus (les quatraines, les huitaines...), il faut un montage combinant 2 demi-additionneurs : l'additionneur complet.
2.2. Additionneur complet
Il permet
l'addition des bits de poids quelconque (rang n > 0) de deux
nombres
binaires en tenant compte d'une retenue Rn
-1
éventuelle provenant du calcul d'une colonne
précédente (rang n - 1).

Le montage de l'additionneur met en oeuvre 2 demi additionneurs et une porte OU selon le schéma ci-dessous :

Répérer les 2 demi additionneurs et la porte OU.
2.3.
Application
: addtionneur 2 bits
Le montage de l'additionneur met en oeuvre 2 demi additionneurs et une porte OU selon le schéma ci-dessous :

Répérer les 2 demi additionneurs et la porte OU.
Il s'agit de réaliser
l'addition de 2 nombres binaires de 2
bits, notés A et B.
A = A1A0 et B = B1B0
Exemple : si A = 10 alors A1 = 1 et A0 = 0 et A vaut 2 en décimal. Si A = 11, alors A1 = 1 et A0 = 1 et A vaut 3 en décimal.
L'addition se présente de la façon suivante :
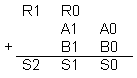
On obtient S0 et R0 grâce à un montage 1/2 additionneur (voir + haut).
En terminant l'addition selon les 2 valeurs possibles pour R0 (à savoir 0 ou 1) on obtient le tableau ci-dessous :
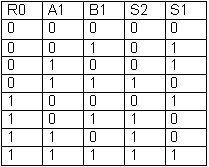
a/ Vérifier rapidement ce tableau en additionnant R0, A1 et B1 dans chaque ligne.
Câbler un additionneur 2 bits sur platine mille trous serait assez fastidieux...comme le montre le schéma du montage :

b/ Cliquer ici (choisir ouvrir ou exécuter) pour simuler ce montage avec Crocodile Physics. Vérifier quelques additions (on ne peut pas faire mieux que 3 + 3 ...)
A = A1A0 et B = B1B0
Exemple : si A = 10 alors A1 = 1 et A0 = 0 et A vaut 2 en décimal. Si A = 11, alors A1 = 1 et A0 = 1 et A vaut 3 en décimal.
L'addition se présente de la façon suivante :

On obtient S0 et R0 grâce à un montage 1/2 additionneur (voir + haut).
En terminant l'addition selon les 2 valeurs possibles pour R0 (à savoir 0 ou 1) on obtient le tableau ci-dessous :

a/ Vérifier rapidement ce tableau en additionnant R0, A1 et B1 dans chaque ligne.
Câbler un additionneur 2 bits sur platine mille trous serait assez fastidieux...comme le montre le schéma du montage :

b/ Cliquer ici (choisir ouvrir ou exécuter) pour simuler ce montage avec Crocodile Physics. Vérifier quelques additions (on ne peut pas faire mieux que 3 + 3 ...)
2.4. additionneur 4 bits
|
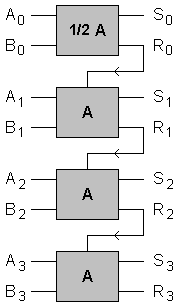
Il
réalise l'addition binaire de deux nombres de 4 bits chacun
: A3A2A1A0
et B3B2B1B0
Voir le montage au bureau pour une démonstration de l'additionneur 4 bits. |
 |
Mathieu 2005 ©